Logical clock algorithms

Logical clock synchronization takes a different approach based on Leslie_Lamport’s 2 observations:

1. The clocks do not really need to agree on time if there is no interaction
2. In fact, the clocks do not even need to synchronize with the real time, they only need to agree on the order in which events occur where event is the result of some action executed by the system itself.

Therefore, we can avoid the difficulty of synchronizing the time by instead assigning logical timestamps to events.

Lamport’s logical clock

Lamport’s logical clock (or timestamp) was proposed by Leslie Lamport in the 1970s and widely used in almost all distributed systems since then, almost all cloud computing systems use some form of logical ordering of events.

Lamport define the relation happens-before (->) between any pair of events with 3 rules:

1. If a and b are events on the same process, then a -> b if a occurs before b based on the local clock.
2. If a process sends a message m to another process, then send(m) -> receive(m) where send(m) and receive(m) are events from first and second processes respectively.
3. happens-before is transitive, i.e. if a -> b and b -> c then a -> c.

The goal of Lamport’s logical clock is to assign timestamps to all events such that these timestamps obey causality - if an event B is caused by an earlier event A, then everyone must see A before seeing B. Formally, if an event A causally happens before another event B, then timestamp(A) < timestamp(B). The timestamp must always go forward and not backward.

Let’s look at an example where 3 processes in the system with the following conditions:

1. We assume the clocks use local counter which is an integer (initial value of counter is 0) but the increment of each clock is different.
2. A process increments its counter when an even happens or when it sends message. The counter is assigned to the event as its timestamp., the message event also carries its timestamp.

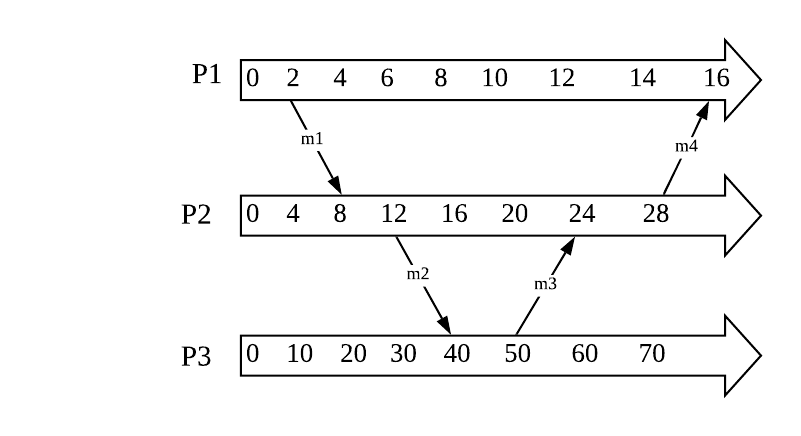
The messages m1 and m2 obey happens-before, however messages m3 and m4 do not and we need to correct the local clock. For example, m3 is sent at 50, them m3 should only be received at 51 or later. The algorithm to update Lamport’s counter is:

1. Before executing an event, the process A increment its counter, i.e. timestamp(A) = timestamp(A) + increment.
2. When A sends a message to process B, it sends along timestamp(A).
3. Upon receiving the message, B will adjust local clock and the counter is then incremented by 1 before the message is considered received., i.e. timestamp(B) = max(timestamp(A), timestamp(B)) + 1.

Sometimes, we do not want 2 events to occur at exactly the same time. In this case, we need to use the unique identifier to break tie, i.e. an event at process A at timestamp 10 is timestamped as (10, A); so if A<B then (10,A) < (10,B) .

On the other hand, if events happen from different processes and do not exchange message directly or indirectly, then nothing can be said about their relation, and these events are said to be concurrent. Concurrent events are not casually related and their order is not guaranteed.

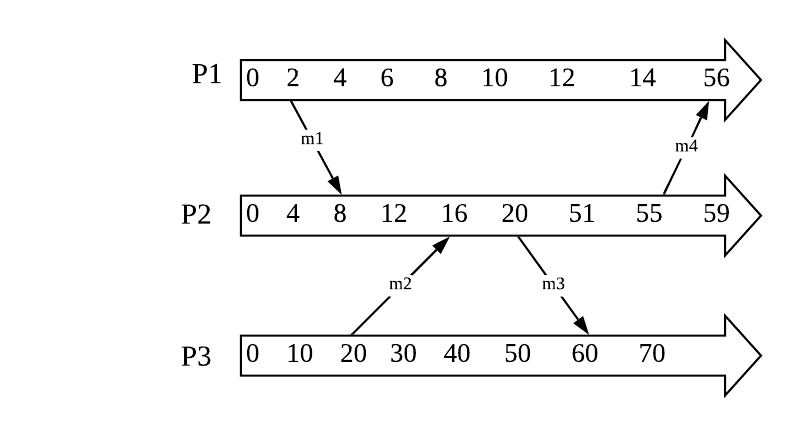
From the example above, for every message, a process needs to send first before the other receives, and timestamp(send) < timestamp(receive) for every message. In the case of the same process, for instance at process 2, we know that the receiving of message 1 happens before the sending of m3, hence timestamp(receive_1) < timestamp(send_3). However by construction, timestamp(receive_1) < timestamp(send_2) but nothing can be said about the sending of m2 and receiving of m1

Hence, Lamport’s logical timestamps obey the rule of causality but cannot distinguish between casual and concurrent:

• If 2 events follow the happens-before relationship, i.e. E1 -> E2 then timestamp(E1) < timestamp but
• timestamp(E1) < timestamp (E2) implies either (E1 < E2) or (E1 and E2 are concurrent)

Vector clock

The vector clock tries to overcome the shortcoming of the logical clock. Suppose there are N presses in the system, each process uses a vector of integer clocks where each vector has N elements, We denote the vector maintained by process i as Vi [1…N], the jth element of the vector at process i, Vi[j], is i’s acknowledgment of latest events at process j.

Vector Clock algorithm to assign and adjust vector timestamp in each process:

1. On an instruction or send event at process i, it increments only its i-th element of its vector clock
2. When a process sends a message, it attaches along its’ vector clock
3. When a process j receives a message from process i, it increase its’ j-th element of its own vector clock and update other elements in the vector:
   • V_j[i] = V_j[i] + 1
   • V_j[k] = max(V_i[k], V_j[k]) for k ≠ j

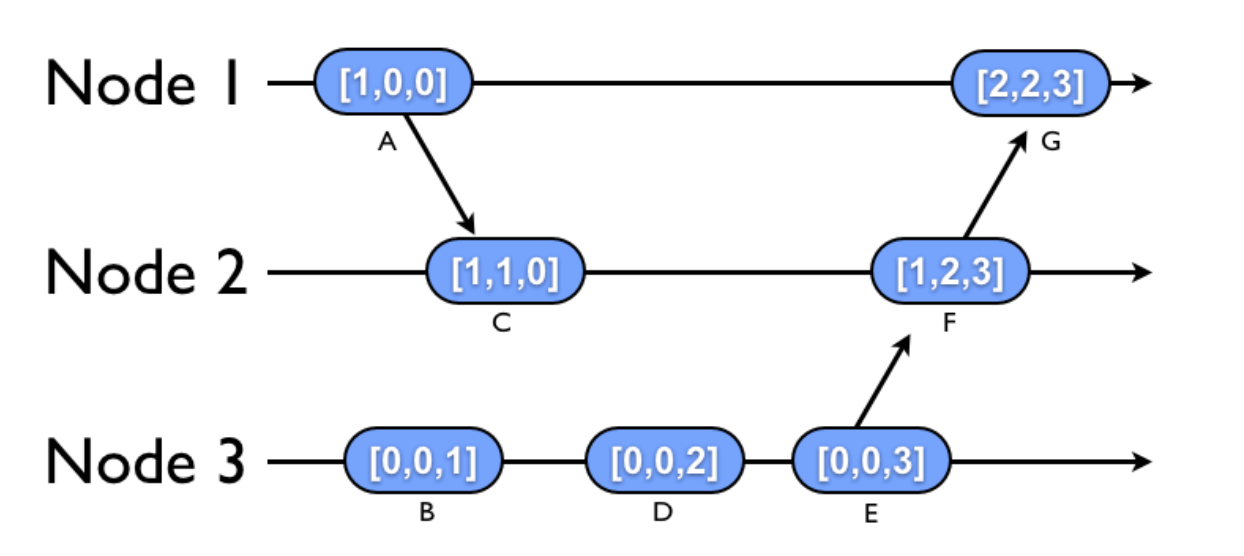
In the example above, mode 1 updates its’ vector to [1,0,0] to represent the event of sending at A before sending to node 2. Upon receiving, node 2 updates the event of receiving at C. When node 2 receives another message at F, it again updates the event of receiving and then adjust other elements in the vector.

Using vector clock, we define some relationships of 2 events a and b:

• V_a = V_b if and only if V_a[i] = V_b[i], for all i = 1, … , N
• V_a ≤ V_b if and only if V_a[i] ≤ V_b[i], for all i = 1, … , N
• a and b are causally related if V_a < V_b if and only if V_a ≤ V_b and there exists j such that 1 ≤ j ≤ N and V_a[j] < V_b[j]. So in the example above, using vector clock, node 2 can tell that message A->C and E->F are casually related.
• a and b are concurrent if and only if NOT (V_a ≤ V_b) AND NOT (V_a ≤ V_b)

Vector clock is is used in key-value stores like Riak.